[最も好ましい] 数学 関数 グラフ 469353-数学 関数 グラフ 面積

二次関数のグラフは全て相似 数学 二次関数 そーまのブログ屋さん
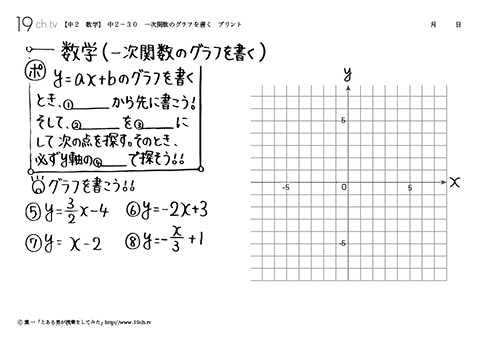
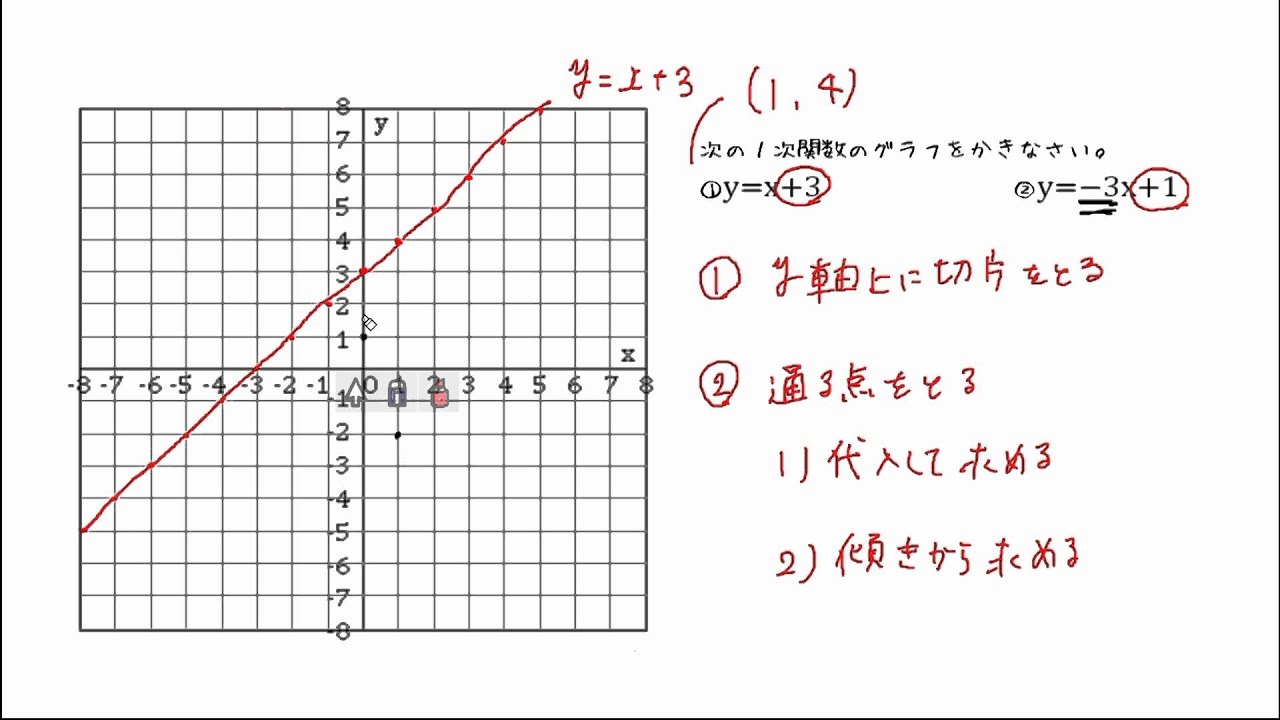
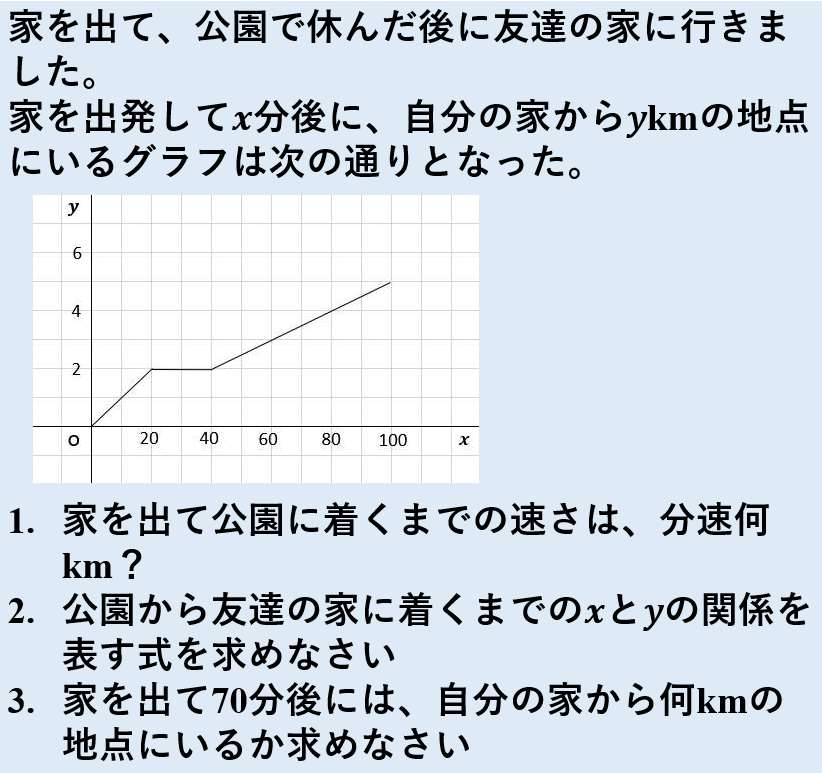
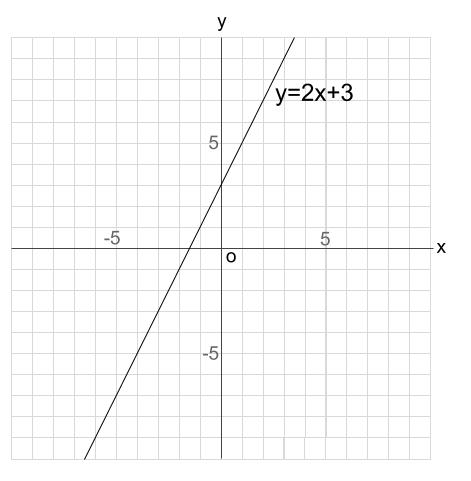
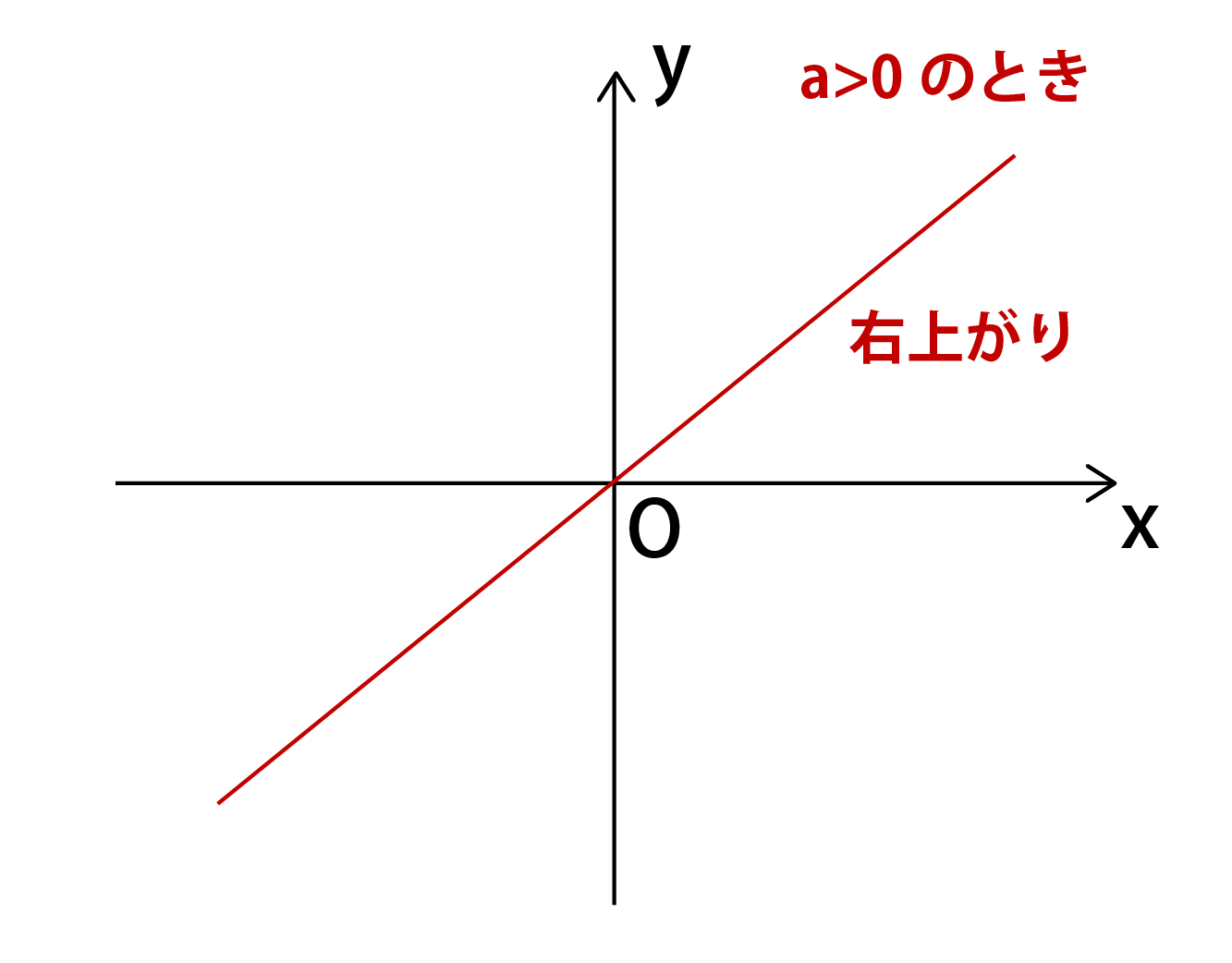
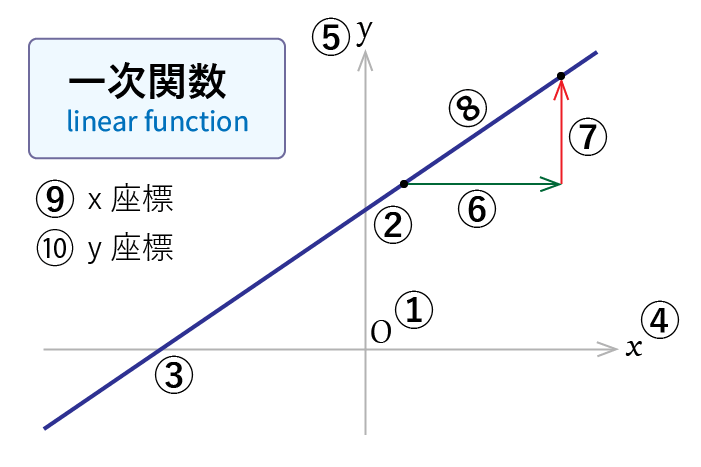
変化の割合 = 傾き 1次関数 y= axb y = a x b において、 a a は、直線の傾きを表している ことを上で見ました。 この a a には別名があり、 変化の割合 といいます。 変化の割合とは、グラフがどのように変化しているのかを示す値で、 変化の割合 = yの10ミリと5ミリの方眼ノートと、数学で関数のグラフをかく練習をするのに便利な数学の関数グラフ練習用方眼ノートです。 「数学の関数グラフ練習用方眼ノート」は、管理人が中学2年生の娘とテスト勉強を一緒にやっている時に、1次関数のグラフをかく練習をやりたくて作りました。 このページの用紙はすべてサイズです。 方眼の目盛りの10ミリ、5ミリのサイズ
数学 関数 グラフ 面積
数学 関数 グラフ 面積-数学の中でも関数はグラフを読みとり、 計算し、考える学力が必要になります。 グラフの問題を攻略するコツは 自分の手でしっかりグラフを書くことです。 わざわざ自分の手で問題を書くのは、 グラフをイメージとして頭の中に残しておくため です。 グラフが苦手な中学生に、「グラフある式をグラフにすると、ハート型の図形を描くことができます。 ハート以外にも、ピカチュウやマリオなどをグラフで描くことができます。 関数のグラフって、書けるようになった? はい。 なんとか人並みには じゃあ、この式のグラフ、書ける? 難しすぎません? あ、やっぱり(笑) じゃあパソコンに書いてもらおう!

Print広場 Studyaid D B 周年 数研出版
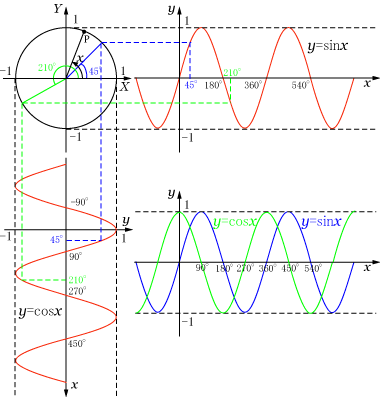
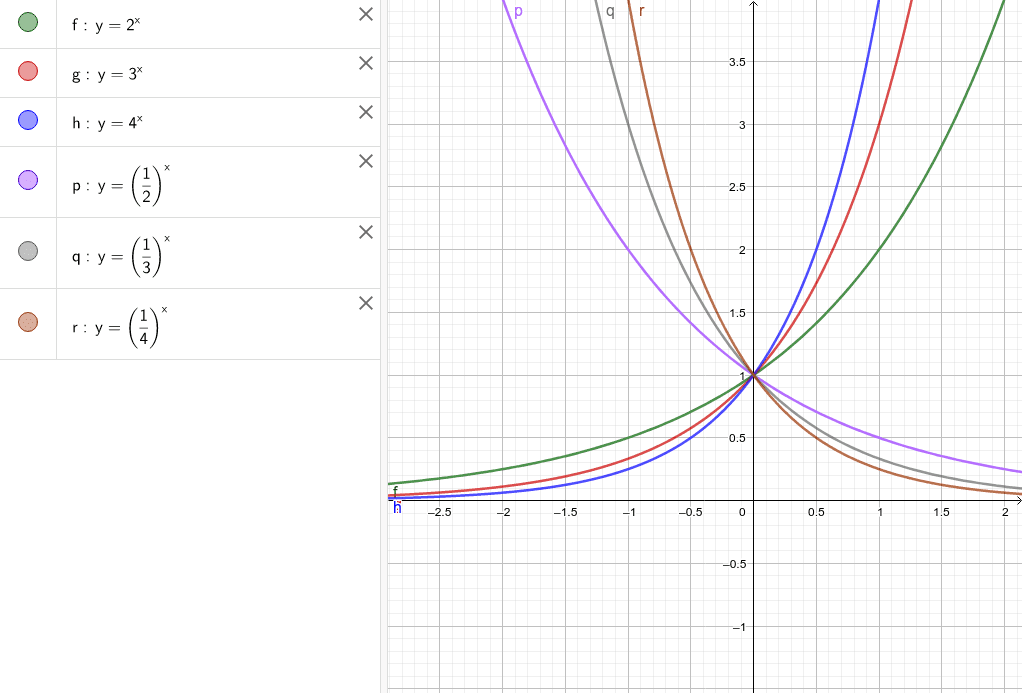
四次関数のグラフの特徴,書き方について解説します。四次関数は,教科書では数学2の発展事項として扱われています。 → 四次関数のグラフの概形と例題2問 陰関数と陽関数の意味と違いについて 陽関数と陰関数の定義: 陽関数 : y = f (x) y=f(x) y = f (x) といういつもの形で表した関数 まとめ expの微分の公式やグラフは?やeの意味や読み方について解説数学 ここでは、 指数関数のexpやeの意味や読み方、計算方法やグラフ、微分の公式 について解説しました。 指数関数expの扱いは意外と難しいのでこの機会に覚えておくといいです。 中学関数のグラフは3パターンのみ 中学校で習う関数のグラフは、ずばり、次の 3つの形 しかありません! ・直線 (比例、一次関数) ・双曲線 (反比例) ・放物線 ( y = ax2 ) ↑ 比例のグラフ( 直線 ) ?↑ 一次関数のグラフ( 直線 )
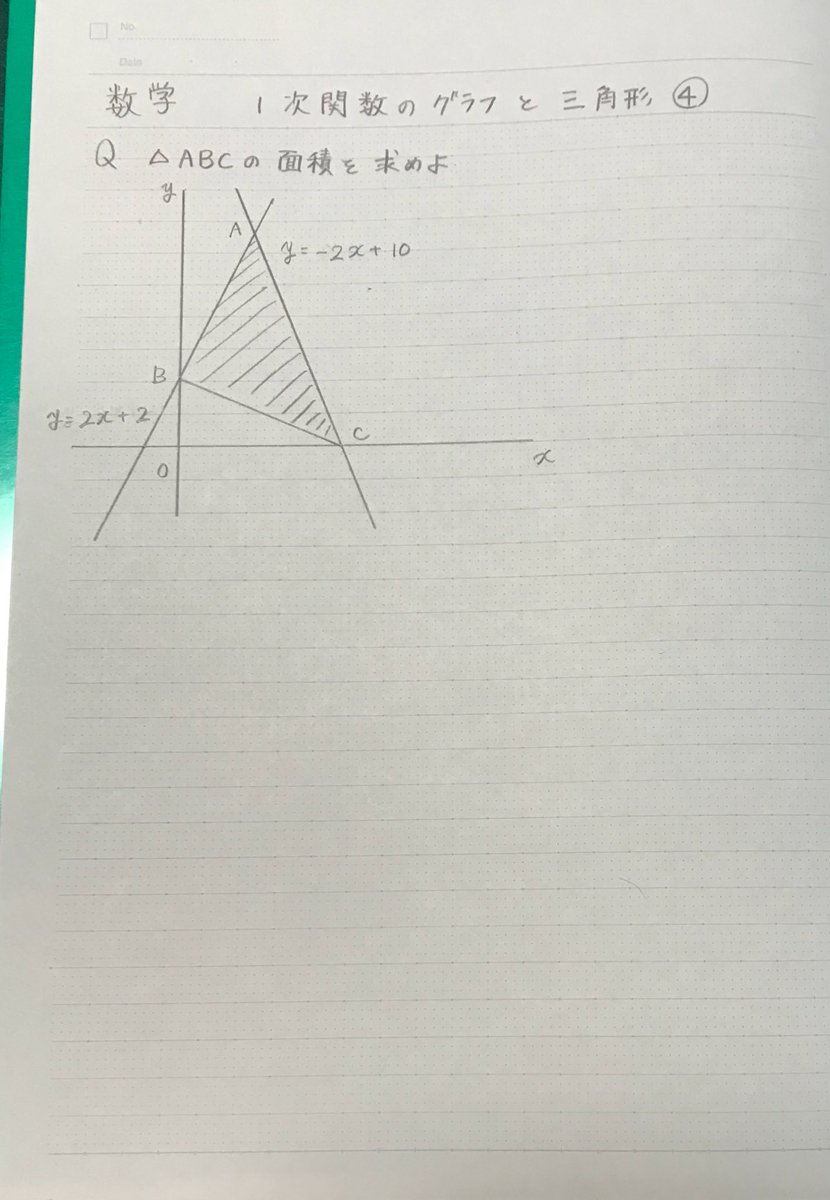
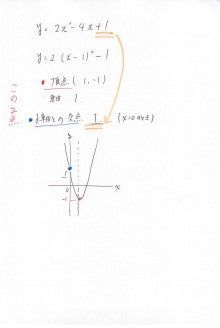
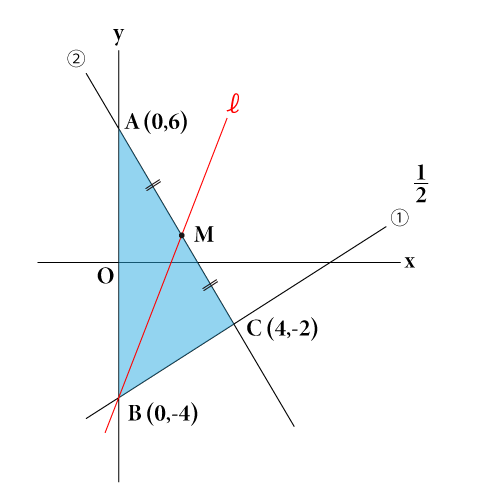
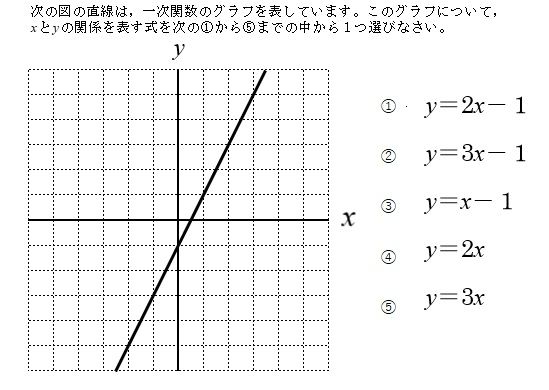
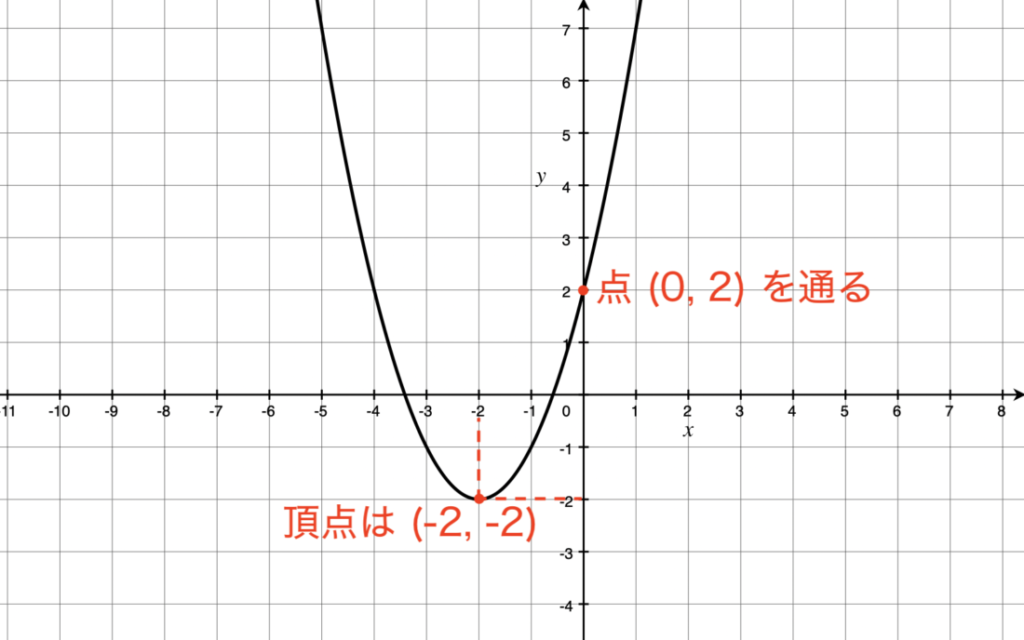
2次関数のグラフ (1) 数学を、数我苦から、数楽へ 高曽章(Koso Akira) ' 2次関数 (1) 2次関数 (2) 2次関数 (3) 2 関連ツイート4 グラフから式を求める 41 グラフから式を求める基本 42 切片がわからないグラフ発展 5 一次関数の変域を求める 51 変域を求める問題の解き方関数y=ax2乗放物線グラフの書き方はこれでバッチリ! RECOMMEND こちらの記事も人気です。 yはxの2乗に比例する関数 中3数学y=ax2乗の変域の求め方を解説! yはxの2乗に比例する関数 中学数学放物線と直線の面積を求める公式は? yはxの2乗に比例する関数 中
数学 関数 グラフ 面積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 | ||
 |  |  |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 |  |  |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | 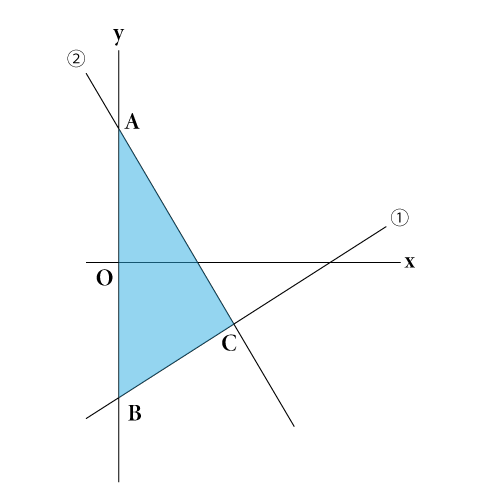 |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
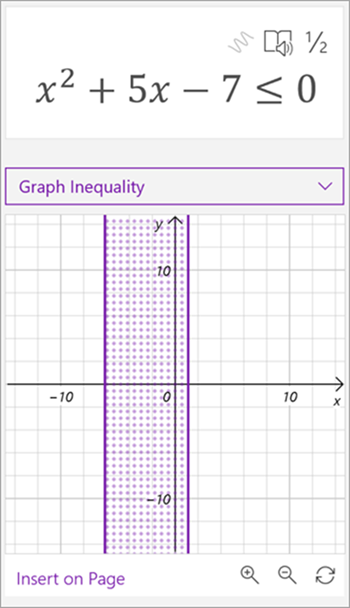 |  |  |
 | 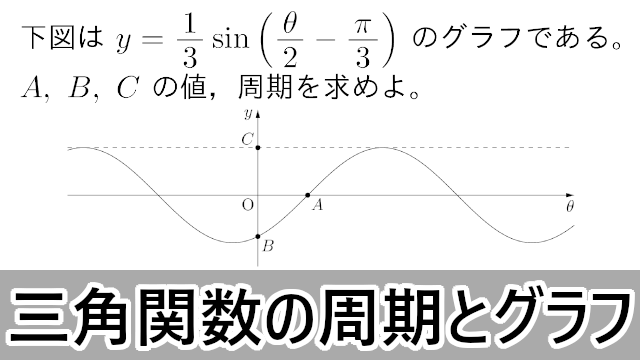 |  |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | 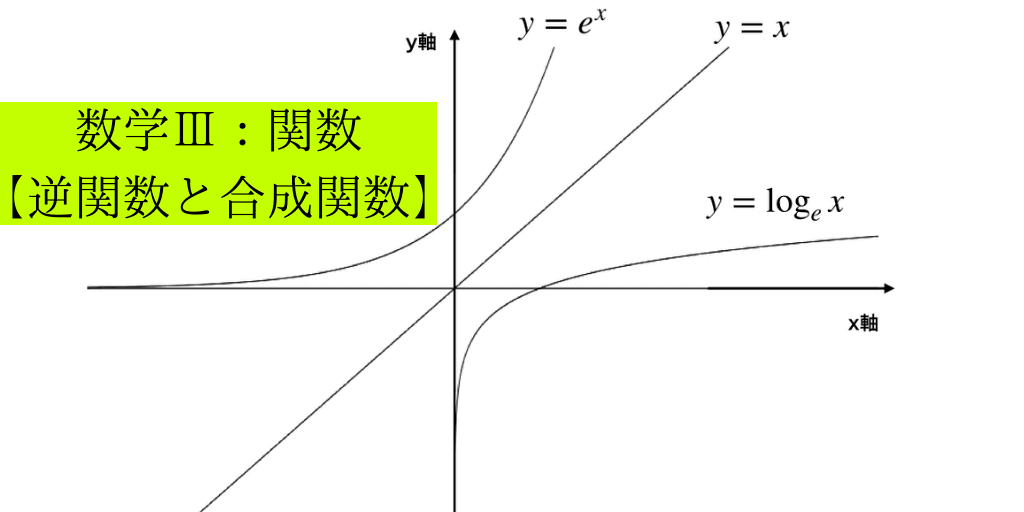 | |
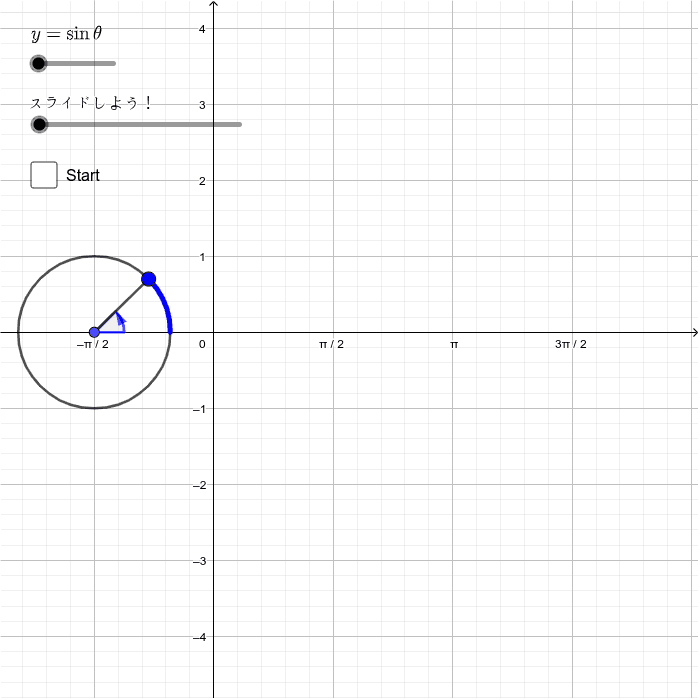 | 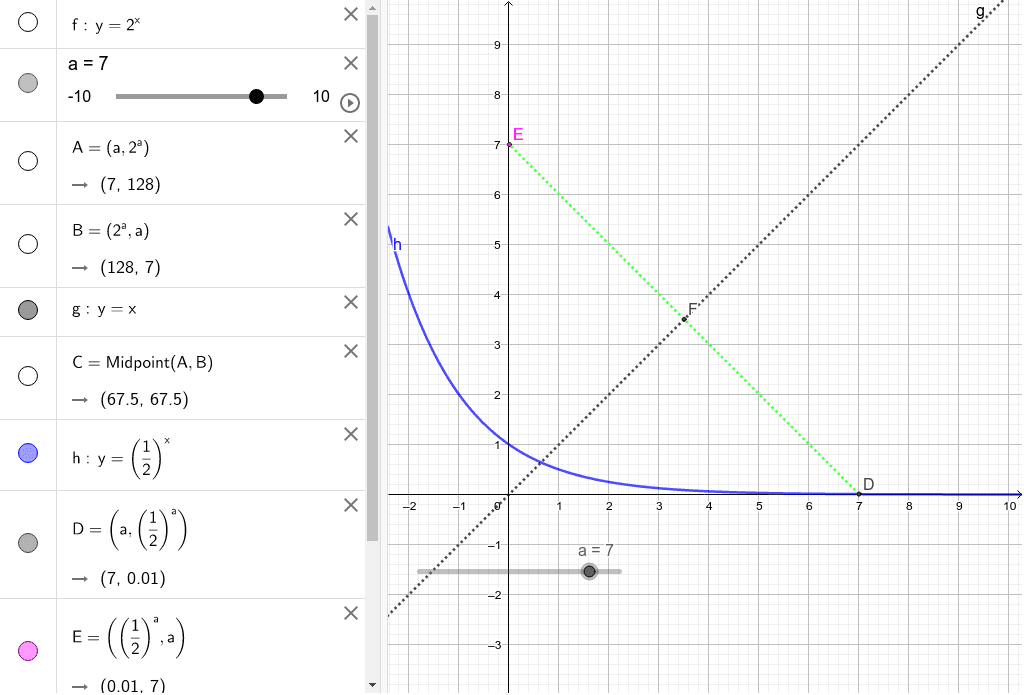 |  |
 |  | |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
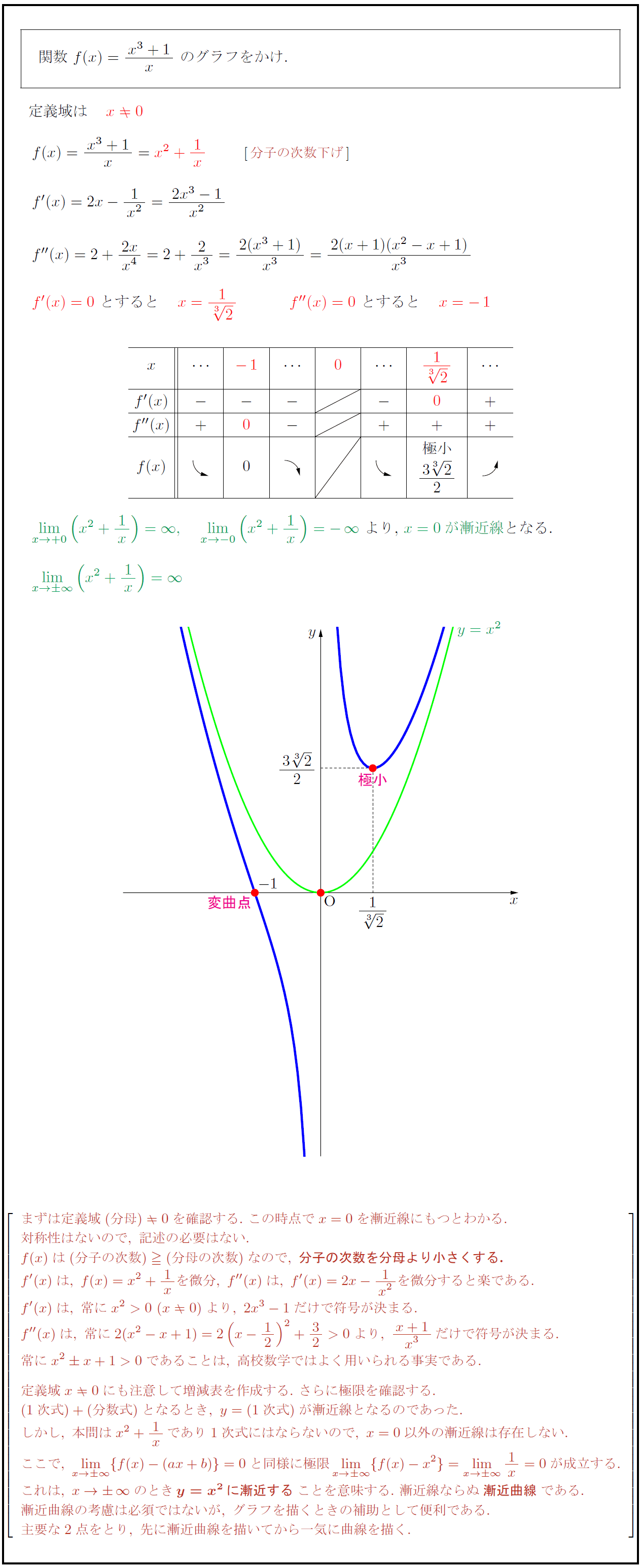 |  | |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「数学 関数 グラフ 面積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |
こういうときは、「もともと x = 0 x = 0 の場合は除かれている」と考えるのがコツだよ。 これを「 定義域 (ていぎいき) 」と言い、反比例のグラフでは特に注意しよう。 つまり x = 0 x = 0 という値を代入しても( 1 1 つの入力)、 y y の値が決まらない( 0 0 つの出力)と関数とは言えないため、 x = 0 x = 0 の場合は除かなくてはいけない、ということになります。 y = 4 xY=ax^2のグラフ(下に凸、上に凸) step1 ポイント y=ax^2のグラフ(下に凸、上に凸) 高校数学Ⅰで学ぶ「y=ax^2のグラフ(下に凸、上に凸)」のテストによく出るポイントを学習しよう! step2 例題 y=ax^2のグラフ(下に凸、上に凸) 高校数学Ⅰで学ぶ「y=ax^2のグラフ(下に凸、上に凸)」のテストによく出る問題(例題)を学習しよう!
Incoming Term: 数学 関数 グラフ, 数学 関数 グラフ 面積, 数学 関数 グラフ 種類, 数学 関数 グラフ 解き方, 数学 関数 グラフ 問題, 数学 関数 グラフ用紙, 数学 関数 グラフ 一覧,
コメント
コメントを投稿